 Phasing
Techniques
Phasing
Techniques Phasing
Techniques
Phasing
TechniquesThe Phase Problem - A Basic Review
In a X-ray diffraction experiment, electrons of the ordered atoms in a crystal diffract the X-rays in defined directions of space. We measure the intensities of each reflections by recording the diffraction pattern on a detector. To reconstruct the electron density (and thus the shape of the atoms and molecules diffracting the X-rays) by Fourier transformation, however, we need TWO components for each reflection:

The absence of phase information poses a serious problem to the otherwise straightforward reconstruction of the electron density p(xyz) from the experimental structure factor amplitudes |Fhkl|.
As a matter of fact, the phases a (hkl) contain a most critical amount of information. Visit the Fourier Duck and it's new friend to show you more about this disturbing feature.
If we can measure only intensities - are we stuck?
Well, not quite yet. Let us recall what we actually measure. The intensity I of a reflection is proportional to the square of the complex structure factor F: I ~ F2 , and F2 = |F|2
F of a reflection (Fhkl) itself is a summation, over all atoms in the crystal unit cell, consisting of TWO terms again: the atomic scattering factor, f, of each atom, and the positional (structural) term for that atom.
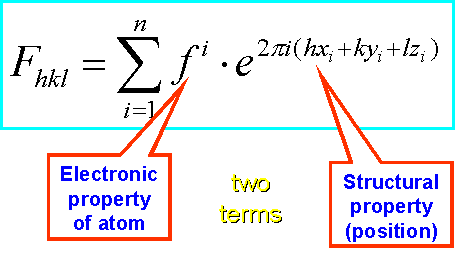
Obviously, we can mathematically separate the position of an atom from its type. What does this knowledge practically mean?
Simplifying the case
Let us assume we could replace one atom in the crystal (usually a water atom) with a heavy metal atom (the big red one), without destroying the crystal, thus keeping the structure the same. Such a procedure, called isomorphous replacement, is actually possible by soaking a protein crystal, which consists to about 50% of solvent, in a heavy metal solution. We can now imagine in real space creating a 'difference crystal' by subtracting the native crystal from the derivative crystal :
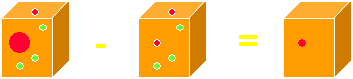
Apparently, we have reduced the problem to a much simpler one : in real space, out imaginary difference crystal would contain only the heavy atom (minus some contribution from whatever it has replaced). The same scenario is conceivable in reciprocal space with a diffraction pattern :

The resulting difference pattern contains still as many reflections, but they originate from the heavy atom only in the crystal structure. Note that a prerequisite for this subtraction of patterns is that they remain isomorphous, i.e., we do not change the structural terms in the structure factor summation.
Finding the heavy atoms 
The benefit of a diffraction pattern created by a single atom (or a few) is that we can actually find its positions, and therefore the phases. We still cannot use a Fourier synthesis to fins the electron density of the heavy atoms, because we still lack their phases. But we can create a phase-less Patterson synthesis, based on the Intensities (not the square root) of the reflections. This map contains peaks at the distance vectors between atoms in the structure. The peak height is proportional to the mean square of the electrons (z) of the atoms located at the ends of the vector (this is why we prefer heavy atoms like Hg, Pt, Au for soaking) and the number of peaks P = N2 - N (N is the number of atoms in the structure). P gets large very rapidly, and for ease of interpretation we want only few atoms in the derivative. Some sophisticated methods can actually solve quite large numbers of atoms, up into the hundreds. This is mostly important for MAD phasing. Once heavy atom positions of two derivatives are determined, MIR phasing equations can be solved and initial protein phases determined.
Another source of electronic differences

The electronic differences needed to create difference maps from which the heavy atom positions and initial protein phases can be solved, can originate from ANY kind of differences in scattering behavior. One powerful approach is to utilize the change of the scattering factor of a heavy (or not so heavy) atom around its X-ray absorption edge. To conduct such a MAD (Multi-wavelength Anomalous Dispersion) experiment, we need to be able to change the wavelength of the X-ray beam used in the diffraction experiment. This is usually done at a synchrotron, where narrow bandwidth monochromators are used to vary the wavelength of the synchrotron radiation emanating from an electron beam circling in a storage ring. The method also creates difference maps between and within data sets recorded at different wavelengths which are solved and usually quite excellent protein phases are obtained. Learn more about the MAD method here.
Other ways to solve the phase problem/Patterson Maps
Information about phases is also contained directly in the intensities. Small molecule crystallography, which a limited number of atoms (few hundred) and atomic resolution data use routinely direct methods. Direct methods are of interest to the macromolecular crystallographer, because they also work well with low resolution difference data if there are few atoms (and larger distances between them). SHELXS and SHELXD (a combination of direct reciprocal and real space methods) are the most popular ones. Patterson maps can also be solved by correlation methods (XtalView) or Patterson vector superposition. SOLVE uses a combination of techniques to find a consistent set of Patterson solutions.
Another way to solve a structure similar (i.e., structurally homologous) to a known protein structure, is to find a positioning of the search model that fits the experimental data. This is called Molecular Replacement (MR). In this case 'replacement' actually means 'relocation, repositioning'. Conventional methods search first for a rotation solution in Patterson space, and then for a translational solution by correlation in reciprocal space (Amore), others use evolutionary algorithms and perform a fast 6-f correlation search (EPMR). MR solutions sometimes can be tricky and subject to heavy model bias. Again, visit the Fourier Duck and it's friend to show you more about model bias.
Summary
All phasing techniques have in common that they provide a set of initial, approximate phases which are derived from additional experimental data, be it heavy metal derivative crystals (Multiple Isomorphous replacement, MIR), anomalous scatterers (Multiple anomalous dispersion, MAD, homologous structures (Molecular Replacement, MR) or any combination thereof. Return to the index for detailed information on individual phasing methods.
Click here for beautiful experimental maps.
![]() Back to X-ray Tutorial Index
Back to X-ray Tutorial Index
This World Wide Web site conceived and maintained
by Bernhard Rupp.
Last revised
Dezember 27, 2009 01:40